强化学习(三)
2022-09-15
阅读:430
策略评估
概念
在环境模型已知的前提下,对任意的策略 $\pi$,需要估算该策略下的累计折扣奖励的期望以衡量该策略的优劣程度,这就是策略评估($Policy\ Evalutaion,\ PE$),换句话说,策略评估就是计算策略 $\pi$ 下每个状态的状态值方程组法
思想:若状态空间离散,且已知策略 $\pi$ 和状态转移概率 $P$,可以设每个状态值为一个未知数,由公式(3-1)可以得到一个线性方程组,称为贝尔曼方程组,求解这个方程组便可以得到每一个状态值案例:
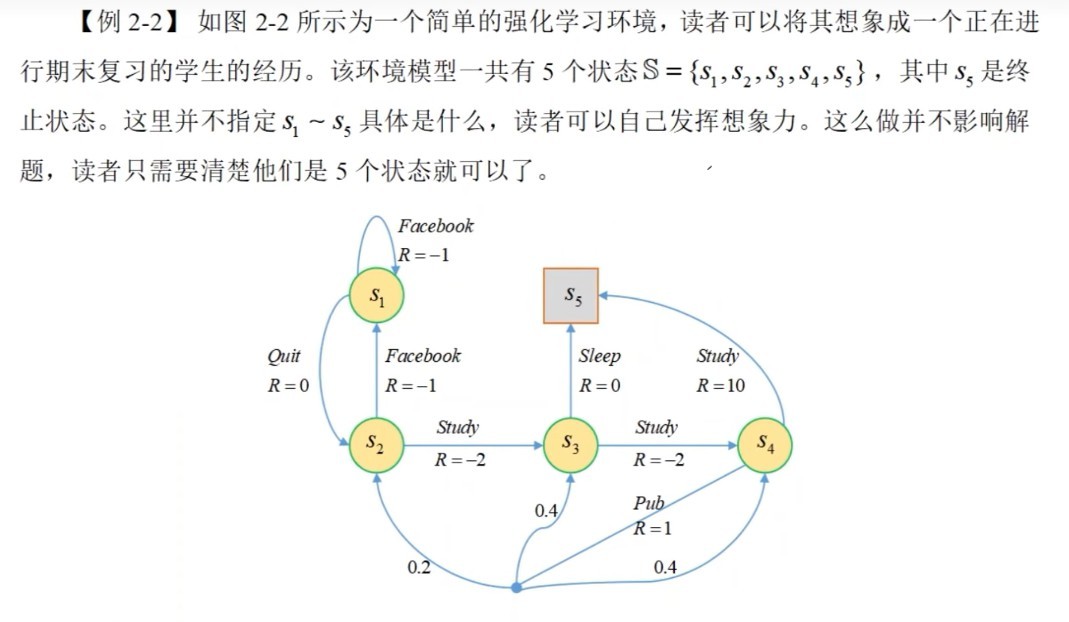
分析:因为已知状态转移概率 $P$,所以这是一个有模型的问题;公式(3-1)就是上一节讲的状态值函数表示的贝尔曼方程
$$
V_\pi(s)=\sum_{a\in A}\pi(a|s)\sum_{s'\in S}P(s'|s,a)(r+\gamma\cdot V_\pi(s')) \tag{3-1}
$$
(1). 状态空间 $S$$$
S=\left\{S1,S2,S3,S4,S5\right\}
$$
(2). 动作空间 $A$$$
A=\{Facebook,Quit,Sleep,Study,Pub\}
$$
(3). 状态转移概率 $P$$$
P(S1|S2,Facebook)=1 \\
~\\
P(S3|S2,Study)=1 \\
... \\
P(S|S4,Pub)=
\begin{cases}
0.2,& \text{S=S2}\\
0.4,& \text{S=S4}\\
0.4,& \text{S=S5}\\
\end{cases}
$$
(4). 奖励函数 $R$$$
R(S1,Facebook,S1)=-1 \\
~\\
R(S1,Quit,S2)=0 \\
... \\
R(S4,Study,S5)=10 \\
$$
(5). 折扣系数 $\gamma$$$
\gamma=1
$$
(6). 平均策略 $\pi$$$
\pi(a|s)=0.5
$$
(7). 基于状态值的贝尔曼方程,根据公式(3-1)$$
V_\pi(S_i)=v_i,\ \ i=1,2,3,4 \\
~\\
V_\pi(S_5)=v_5=0 \\
~\\
\Downarrow \\
~\\
\begin{cases}
v_1=0.5(-1+v_1)+0.5(0+v_2) \\
~\\
v_2=0.5(-1+v_1)+0.5(-2+v_3) \\
~\\
v_3=0.5(0+0)+0.5(-2+v_4) \\
~\\
v_4=0.5(10+0)+0.5(1+0.2v_2+0.4v_3+0.4v_4) \\
~\\
v_5=0 \\
\end{cases}
~\\
\Downarrow 解方程 \\
~\\
\begin{cases}
v_1=-2.3077=V_\pi(S_1) \\
~\\
v_2=-1.3077=V_\pi(S_2) \\
~\\
v_3=2.6923=V_\pi(S_3) \\
~\\
v_4=7.3846=V_\pi(S_4) \\
~\\
v_5=0=V_\pi(S_5)
\end{cases}
$$
迭代法
(1). 思想$$
V_\pi(s)\leftarrow \sum_{a\in A}\pi(a|s)\left(r+\gamma\cdot \sum_{s'\in S}P(s'|s,a)\cdot V_\pi(s') \right) \tag{3-2}
$$
(2). 迭代式策略评估算法(3-3):- 输入:环境模型 $MDP(S,A,P,R,\gamma)$ ,待评估的策略 $\pi$,容忍系数 $\epsilon$(一个很小的正数)
- 初始化:状态值 $V_\pi(s)=0$
- 过程:
- $\qquad$循环:
- $\qquad \qquad$$Delta leftarrow 0$
- $\qquad \qquad $循环:对每一个 $s \in S$
- $\qquad \qquad \qquad $ $\boldsymbol{V\leftarrow V_\pi(s)}$,记录上一个状态值函数
- $\qquad \qquad \qquad $根据公式(3-2),更新本次迭代的状态值 $V_\pi(s)$
- $\qquad \qquad \qquad $更新绝对误差: $\boldsymbol{\Delta\leftarrow max(\Delta,|V-V_\pi(s)|)}$
- $\qquad \qquad $如果 $\Delta < \epsilon$ 则结束循环,否则继续下一轮循环
- 输出:状态评估值 $V_\pi(s)$
参考
最后编辑于:2022 年 09 月 26 日 09:21
