深度强化学习(十六)
2022-09-27
阅读:744
神经网络值函数近似法
DQN 算法
将深度神经网络近似的动作值函数嵌入到 $Q-learning$ 算法框架就得到 $Deep\ \ Q-learning$ 算法,简称$DQN$Q 网络
一般有如下三种 $Q$ 网络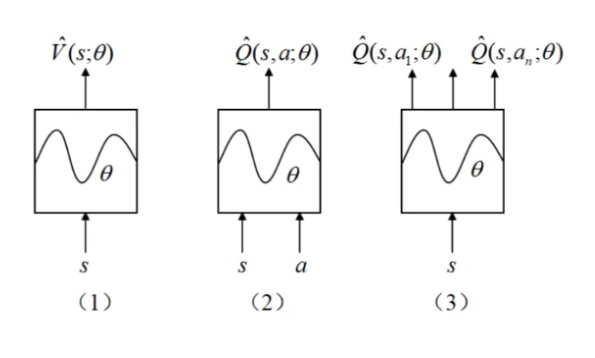
网络(1)输入是一种状态 $s$,输出是对状态值函数的近似 $\hat{V}(s;\theta)$
网络(2)输入是一种状态动作对 $(s,a)$,输出是对动作值函数的近似 $\hat{Q}(s,a;\theta)$
网络(3)输入是一种状态 $s$,输出是所有状态值函数的近似 $\hat{Q}(s,a_1;\theta),\cdots,\hat{Q}(s,a_n;\theta)$
相对来说,网络 $2$ 和 $3$ 比较常用,$2$ 的近似更准确一些,$3$ 的近似更广泛一些
网络 $1$ 和网络 $2$ 同时适用于连续空间和离散空间;网络 $3$ 同时适用于连续状态空间和离散状态空间,但只适用于离散动作空间
损失函数
跟线性值函数近似法一样,损失函数是目标值 $Q$ 与预测值 $\hat{Q}$ 差值的期望 $L(\theta)$$$
L(\theta)=E_{\pi}\left[\left(Q_{\pi}(s,a)-\hat{Q}_{\pi}(s,a;\theta)\right)^{2}\right]
~\\
Q_{\pi}(s, a) \approx R(s, a)+\gamma\ \hat{Q}_{\pi}\left(s^{\prime}, a^{\prime} ; \theta\right) \tag{16-1}
$$
经验回放技术
结合深度学习和强化学习:强化学习没有训练数据(标签)的,数据(样本)是实时交互得到的,但深度学习是需要训练数据的,故提出经验回放技术(Experience Replay)来解决这个问题在 $Agent$ 与环境交互的过程中,将全部交互数据保存下来,在训练损失函数的时候,就从保存下来的经验数据中选择可以作为训练样本的数据片段,将它们作为训练数据进行训练
在每个交互回合($Iteration$)中
$$
s_t,s_t \stackrel{产生}\longrightarrow R_{t+1},s_{t+1},end
$$
将这样的数据片段称为经验数据,储存起来,形成经验回放池$$
\{(s,a,R,s',end)_t\} \quad t=0,\cdots,T
$$
训练的时候如何使用?输入数据:$(s,a)$,输出数据:公式(16-1)中的 $TD$ 目标值 $Q_\pi(s,a)$
$$
y=
\begin{cases}
R &end=True \\
~\\
R+\gamma\ max_{a \in A} \hat{Q}(s',a;\theta) &end=False
\end{cases} \tag{16-2}
$$
说明:当结束时,$end=True$,预测值 $\hat{Q}=0$ 所以,训练数据表示为:
$$
\{(s,a),y \}_{t=0}^T \quad or \quad \{(s,a),y \}_{t=1}^{batch}
$$
训练 Q 网络
训练过程就是要调整参数 $\theta$,最小化损失函数$$
L_{B}(\theta)=\frac{1}{B} \sum_{i=1}^{B}\left(y_{i}-\hat{Q}\left(s_{i}, a_{i} ; \theta\right)\right)^{2} \tag{16-3}
$$
拿它对 $\theta$ 求梯度$$
\nabla_{\theta} L=-\frac{2}{B} \sum_{i=1}^{B}\left(y_{i}-\hat{Q}\left(s_{i}, a_{i} ; \theta\right)\right) \cdot \nabla_{\theta} \hat{Q}\left(s_{i}, a_{i} ; \theta\right) \tag{16-4}
$$
说明:(1)$y_i$ 就是目标值 $Q_\pi(s,a) \approx R(s, a)+\gamma\ \hat{Q}_{\pi}\left(s^{\prime}, a^{\prime} ; \theta\right)$
(2)称目标值与预测值之间的差值 $y_{i}-\hat{Q}\left(s_{i}, a_{i} ; \theta\right)$ 为误差
(3)梯度 $\nabla_{\theta} \hat{Q}\left(s_{i}, a_{i} ; \theta\right)=\left(\frac{\partial \hat{Q}}{\partial \theta_{1}}, \frac{\partial \hat{Q}}{\partial \theta_{2}}, \cdots \frac{\partial \hat{Q}}{\partial \theta l}\right)^{\top}$,是对每个分量的偏微分
然后使用梯度下降法
$$
\theta \longleftarrow \theta + \eta \sum_{i=1}^{B}\left(y_{i}-\hat{Q}\left(s_{i}, a_{i} ; \theta\right)\right) \cdot \nabla_{\theta} \hat{Q}\left(s_{i}, a_{i} ; \theta\right) \tag{16-5}
$$
可简化为:$$
\theta \longleftarrow \theta + \eta \cdot \nabla_{\theta} L \tag{16-6}
$$
说明:(1)由于前面算的 $\nabla_{\theta} L$ 中有一个负号,所以是梯度下降用的加号
(2)$\eta \frac{2}{B}$ 可以直接整合为一个数 $\eta$
$\ $
DQN-2013 算法(16-7)
- 输入:环境模型 $MDP(S,A,R,\gamma)$,学习率 $\alpha$,贪婪系数 $\epsilon$,经验回放池容量 $num\_samples$,批量大小 $batch\_size$,最大训练局数 $num\_episodes$
- 初始化:随机初始化 $Q$ 网络参数 $\theta$,初始化经验回放池 $D=\oslash$,初始策略求解 $\pi(s)=\arg\max_{a\in \mathbb{A}} \hat{Q}(s,a;\theta)$
- 过程:
- $\qquad$ $for$:$i=1\sim num\_episodes$
- $\qquad \qquad$ 初始状态:$s=s_0$
- $\qquad \qquad$ 初始化回合结束指示器:$end=False$
- $\qquad \qquad$ $while$:$end==False$
- $\qquad \qquad \qquad$ 根据当前 $\epsilon$ 贪婪策略选择动作:$a=\pi_\epsilon(s)$
- $\qquad \qquad \qquad$ 执行动作:$s,a,R,s',end$
- $\qquad \qquad \qquad$ 升级经验回放池:$D \leftarrow D \bigcup\left\{\left(s, a, R, s^{\prime},end\right)\right\}$
- $\qquad \qquad \qquad$ $if \quad |D| \geq num\_samples$
- $\qquad \qquad \qquad \qquad$ 删除现存最初的经验数据
- $\qquad \qquad \qquad$ $end\ \ if$
- $\qquad \qquad \qquad$ $if \quad |D| \geq batch\_size$
- $\qquad \qquad \qquad \qquad$ 任取一个批量的训练数据 $\{(s,a,R,s',end_i) \}_{t=1}^{batch} \subset D$
- $\qquad \qquad \qquad \qquad$ 计算 $TD$ 目标值:$y_i(\theta)$ 公式(16-2)
- $\qquad \qquad \qquad \qquad$ 用 $\{(s_i,a_i),y_i \}_{t=1}^{batch}$ 作为训练数据训练 $Q$ 网络
- $\qquad \qquad \qquad$ $end\ \ if$
- $\qquad \qquad \qquad$ 状态更新:$s \leftarrow s'$
- $\qquad \qquad$ $end\ \ while$
- $\qquad$ $end\ \ for$
- 输出:最终策略 $\pi^*$,最终动作值 $Q^*$
(1)关于经验回放池,有一个最大容量,如果超出最大容量,则从头开始删除经验片段;是因为网络在逐渐优化,越到后面经验片段会越准确,所以要删除最初的数据
(2)步骤 10~18 相当于策略评估
$\ $
DQN-2015 算法(16-8)
- 输入:环境模型 $MDP(S,A,R,\gamma)$,学习率 $\alpha$,贪婪系数 $\epsilon$,经验回放池容量 $num\_samples$,批量大小 $batch\_size$,最大训练局数 $num\_episodes$,目标 $Q$ 网络更新频率参数 $c$
- 初始化:初始化预测 $Q$ 网络参数 $\theta$,初始化目标 $Q$ 网络参数 $\theta’=\theta$,初始化经验回放池 $D=\oslash$,初始策略求解 $\pi(s)=\arg\max_{a\in \mathbb{A}} \hat{Q}(s,a;\theta)$
- 过程:
- $\qquad$ $for$:$i=1\sim num\_episodes$
- $\qquad \qquad$ 初始状态:$s=s_0$
- $\qquad \qquad$ 初始化回合结束指示器:$end=False$
- $\qquad \qquad$ 时间步计数器:$k=0$
- $\qquad \qquad$ $while$:$end==False$
- $\qquad \qquad \qquad$ 更新计数器:$k=k+1$
- $\qquad \qquad \qquad$ 根据当前 $\epsilon$ 贪婪策略选择动作:$a=\pi_\epsilon(s)$
- $\qquad \qquad \qquad$ 执行动作:$s,a,R,s',end$
- $\qquad \qquad \qquad$ 升级经验回放池:$D \leftarrow D \bigcup\left\{\left(s, a, R, s^{\prime},end\right)\right\}$
- $\qquad \qquad \qquad$ $if \quad |D| \geq num\_samples$
- $\qquad \qquad \qquad \qquad$ 删除现存最初的经验数据
- $\qquad \qquad \qquad$ $end\ \ if$
- $\qquad \qquad \qquad$ $if \quad |D| \geq batch\_size$
- $\qquad \qquad \qquad \qquad$ 任取一个批量的训练数据 $\{(s,a,R,s',end_i) \}_{t=1}^{batch} \subset D$
- $\qquad \qquad \qquad \qquad$ 计算 $TD$ 目标值:$y_i(\theta')$ 公式(16-2)
- $\qquad \qquad \qquad \qquad$ 用 $\{(s_i,a_i),y_i \}_{t=1}^{batch}$ 作为训练数据训练 $Q$ 网络
- $\qquad \qquad \qquad$ $end\ \ if$
- $\qquad \qquad \qquad$ 状态更新:$s \leftarrow s'$
- $\qquad \qquad \qquad$ $if$:$k\%c==0$
- $\qquad \qquad \qquad \qquad$ 目标网络参数更新:$\theta'=\theta$
- $\qquad \qquad$ $end\ \ while$
- $\qquad$ $end\ \ for$
- 输出:最终策略 $\pi^*$,最终动作值 $Q^*$
(1)以上两个 $DQN$ 算法,不同点就是在于计算 $TD$ 目标值时用到的参数 $\theta$,后者使用 $\theta'$ 来计算
(2)$\theta'$ 和 $\theta$ 并不同步更新,预测网络参数 $\theta$ 还是每个回合都更新,而目标网络参数 $\theta'$ 要经过固定迭代回合 $c$ 后才更新一次;这样做的目的时为了消除自举,让模型迭代若干步后仍然记得之前学习到的经验
参考
最后编辑于:2022 年 09 月 28 日 23:01
