DQN算法变体

现在又两种思路去优化算法

(1).TD Error：$Q' \leftarrow R_{t+1}+ \gamma \cdot \max_{a \in \mathbb{A}}Q(s_{t+1},a_{t+1})$，让 $Q(s_{t+1},a_{t+1})$ 更准确

(2).数据层面：在所有的数据中 $(s,a,R,s',a')$，只利用好的经验数据，那么什么是好的数据？

Double DQN（DDQN）算法

1.贪婪法获得 TD Target（针对思路1优化）

以前的计算 TD Error 的方法：
由于每次都是取 max 最大值，所以会产生一个正向偏置，导致过度估计问题（Over Estimation），最后导致估计不够准确

2.DDQN：解耦最大化操作

第一步：计算一个贪婪动作 $a_{max}'$，基于参数 $\theta$
第二步：基于动作值函数求 $\hat{Q}$
第三步：根据前面两步计算 $y_i$
上述步骤即称为解耦，利用了不同的 $\theta$

DDQN 算法（17-3）

1. 输入：环境模型 $MDP(S,A,R,\gamma)$，学习率 $\alpha$，贪婪系数 $\epsilon$，经验回放池容量 $num\_samples$，批量大小 $batch\_size$，最大训练局数 $num\_episodes$，目标 $Q$ 网络更新频率参数 $c$
2. 初始化：初始化预测 $Q$ 网络参数 $\theta$，初始化目标 $Q$ 网络参数 $\theta’=\theta$，初始化经验回放池 $D=\oslash$，初始策略求解 $\pi(s)=\arg\max_{a\in \mathbb{A}} \hat{Q}(s,a;\theta)$
3. 过程：
4. $\qquad$ $for$：$i=1\sim num\_episodes$
5. $\qquad \qquad$ 初始状态：$s=s_0$
6. $\qquad \qquad$ 初始化回合结束指示器：$end=False$
7. $\qquad \qquad$ 时间步计数器：$k=0$
8. $\qquad \qquad$ $while$：$end==False$
9. $\qquad \qquad \qquad$ 更新计数器：$k=k+1$
10. $\qquad \qquad \qquad$ 根据当前 $\epsilon$ 贪婪策略选择动作：$a=\pi_\epsilon(s)$
11. $\qquad \qquad \qquad$ 执行动作：$s,a,R,s',end$
12. $\qquad \qquad \qquad$ 升级经验回放池：$D \leftarrow D \bigcup\left\{\left(s, a, R, s^{\prime},end\right)\right\}$
13. $\qquad \qquad \qquad$ $if \quad |D| \geq num\_samples$
14. $\qquad \qquad \qquad \qquad$ 删除现存最初的经验数据
15. $\qquad \qquad \qquad$ $end\ \ if$
16. $\qquad \qquad \qquad$ $if \quad |D| \geq batch\_size$
17. $\qquad \qquad \qquad \qquad$ 任取一个批量的训练数据 $\{(s,a,R,s',end_i) \}_{t=1}^{batch} \subset D$
18. $\qquad \qquad \qquad \qquad$ 计算 $TD$ 目标值：公式（17-2）
19. $\qquad \qquad \qquad \qquad$ $y_i=\begin{cases}R_i &end=True \\ R_i+\gamma\ \hat{Q}(s_i',\arg\max_{a \in \mathbb{A}}\hat{Q}(s_i',a;\theta);\theta') &end=False \end{cases}$
20. $\qquad \qquad \qquad \qquad$ 用 $\{(s_i,a_i),y_i \}_{t=1}^{batch}$ 作为训练数据训练 $Q$ 网络
21. $\qquad \qquad \qquad$ $end\ \ if$
22. $\qquad \qquad \qquad$ 状态更新：$s \leftarrow s'$
23. $\qquad \qquad \qquad$ $if$：$k\%c==0$
24. $\qquad \qquad \qquad \qquad$ 目标网络参数更新：$\theta'=\theta$
25. $\qquad \qquad$ $end\ \ while$
26. $\qquad$ $end\ \ for$
27. 输出：最终策略 $\pi^*$，最终动作值 $Q^*$

说明：DDQN 与 DQN 只有步骤 19 不同

Prioritized Replay DQN 算法

带优先级的经验回放池（基于思路2优化）

样本优先级

定义经验数据优先级 $\left|\delta_{i}\right|=\left|y_{i}-\hat{Q}\left(s_{i}, a_{i} ; \theta\right)\right|$

优先级的定义应该满足两个条件：

（1）优先级在数值上应该和误差绝对值成单调递增关系，这是为了满足误差绝对值较大（即优先级较大）的样本获得更大的被抽样的机会

（2）优先级数值应大于0，这是为了保证每一个样本都有机会被抽样，即抽样概率大于0

基于比例的样本优先级

第 $i$ 个样本的优先级
第 $i$ 个样本被采样的概率，$\alpha \in [0,1]$ 决定的是这个优先级起作用的程度
$\alpha=1$，就完全按照优先级采样概率；$\alpha=0$，就按照均匀分布采样概率

基于排序的样本优先级

$rank(i)$ 代表第 $i$ 个样本的排序位置
第 $i$ 个样本被采样的概率同上公式（17-5）

随机优先级采样

采样方法

（1）贪婪优先级采样（Greedy Prioritization Sampling）：$\alpha = 1 \quad P(i)=\frac{P_i}{\Sigma_k P_k}$

（2）一致随机采样（Uniform Random Sampling）：$\alpha = 0 \quad P(i)=\frac{1}{\Sigma_k 1}=\frac{1}{k}$

（3）随机优先级采样（Stochastic Prioritization Sampling）：完全随机

采样的两个基本原则

（1）样本被采样的概率应该和样本优先级成正相关关系

（2）每一个样本都应该有机会被采样，即被采样的概率大于0

Dueling DQN 算法

Dueling DQN 是将动作值函数 $Q(s,a)$ 的计算分解成两部分：状态值和优势函数（基于思路1优化）
这里，$A(s,a)$ 称为优势函数（Advantage Function），它反映了在状态 $s$ 下的动作值函数 $Q(s,a)$ 和所选动作 $a$ 的相关关系

优势函数的性质

（1）在某一策略 $\pi$ 下，优势函数关于分布 $a \sim \pi(s \mid a)$ 的期望为0
（2）对于确定性策略 $\pi$（贪婪策略），在状态 $s$ 下所选定的动作 $a'=\pi(s)$ 的优势函数 $A(s,a)=0$
Dueling DQN 网络示意图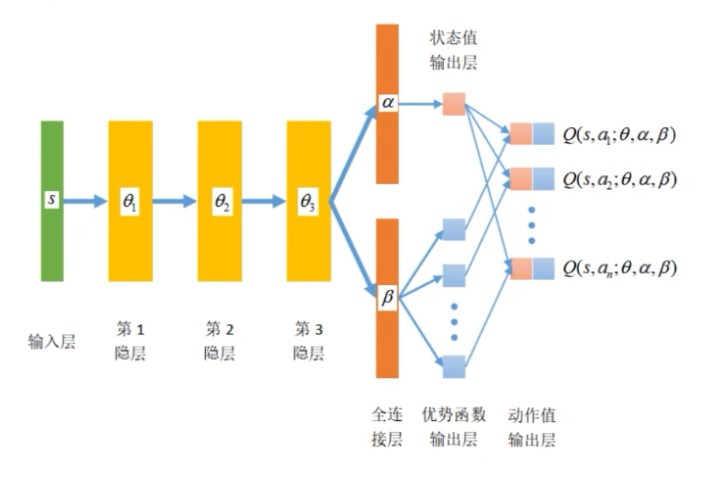

参考

• https://github.com/QiangLong2017