强化学习(六)
2022-09-17
阅读:638
值迭代与策略迭代
策略迭代
(1). 算法思想: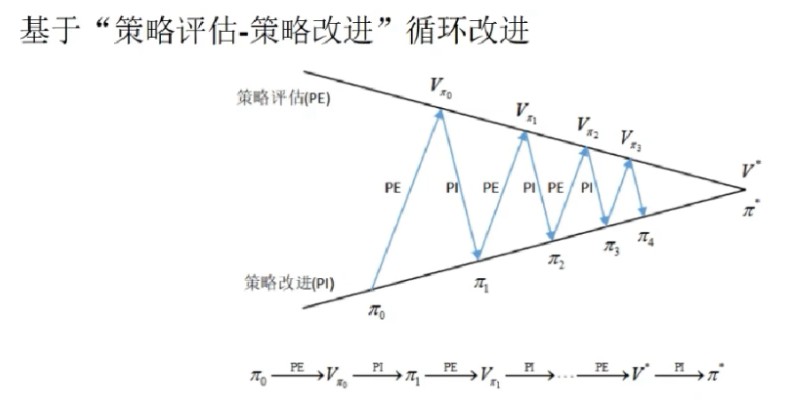
(2). 策略迭代算法(6-1)
- 输入:环境模型 $MDP(S,A,P,R,\gamma)$
- 初始化:随机初始化策略 $\pi$
- 过程:
- $\qquad$循环:直到连续两(多)次策略相同
- $\qquad \qquad$策略评估:正对当前策略 $\pi$,利用迭代式策略评估算法(3-3)计算状态值 $V_\pi(s)$
- $\qquad \qquad$策略改进:利用贪婪策略改进算法策略$\pi$
- 输出:最优策略 $\pi^*$,最优状态值 $V^*$
值迭代
(1). 算法思想:利用贝尔曼最优性方程1.基于状态值函数:
$$
V(s)\longleftarrow \max_{a\in A} \sum_{s\in S}P(s'\mid s,a)\left[r+\gamma\cdot V(s') \right] \\ \tag{6-2}
~\\
V_1 \rightarrow V_2 \cdots \rightarrow V_*\ 最优状态值
$$
2.基于动作值函数:$$
Q(s,a)\longleftarrow \sum_{s'\in S}\left(r+\gamma\cdot \max_{a'\in A}Q(s',a') \right) \\
~\\
Q_1 \rightarrow Q_2 \cdots \rightarrow Q_*\ 最优动作值 \tag{6-3}
$$
当得到了最优状态值函数或最优动作值函数后,由公式(4-2)应用一次贪婪策略;其中,前者还需要利用公式(2-4)将状态值转化为动作值$$
Q^*(s,a)=\sum_{s'\in S}P(s'\mid s,a)\left(r+\gamma\cdot V^*(s') \right)
$$
就可以得到最优策略 $\pi^*$$$
\pi^*(s)=\arg\max_{a\in A}Q^*(s,a)
$$
(2). 值迭代算法算法 (6-4)- 输入:环境模型 $MDP(S,A,P,R,\gamma)$,容忍系数 $\epsilon>0$
- 初始化:随机初始化状态值函数 $V(s)$
- 过程:
- $\qquad$ 循环:
- $\qquad \qquad$ $\Delta \leftarrow 0$
- $\qquad \qquad$循环:$s\in S$
- $\qquad \qquad \qquad$ $V\leftarrow V(s)$,记录当前状态值
- $\qquad \qquad \qquad$ 根据公式(6-2)更新状态值
- $\qquad \qquad \qquad$ $\Delta \leftarrow \max(\Delta,\left|V-V(s)\right|)$,维持状态值更新前后的绝对最大差值
- $\qquad \qquad$ 如果$\Delta<\epsilon$,则循环结束,否则开始新一轮循环
- $\qquad$ 最优策略:根据公式(4-2)求出最优策略
- 输出:最优策略 $\pi^*$,最优状态值 $V^*(s)$
(1). 同步更新:在$step\ 7$中,计算出所有的 $V(s)$ 后再更新到下一步计算中
(2). 异步更新:在$step\ 7$中,计算出一个新的 $V(s)$ 后马上更新到下一步计算中
(3). 算法基于状态值函数和动作值函数,迭代的是值函数
(4). 策略迭代和值迭代是强化学习的两个基本框架
参考
最后编辑于:2022 年 09 月 26 日 09:28
