强化学习(四)
2022-09-16
阅读:400
策略改进
策略改进就是利用对当前策略评估得到的状态值函数来计算出一个新的更优的策略那么如果来评估策略的优劣呢?
设 $\pi$ 和 $\pi'$ 为两个策略,若对任意 $s\in S$ 都有 $V_\pi(s)\le V_\pi'(s)$,测称策略 $\pi'$ 不差于 $\pi$,若至少存在一个状态使得严格不等式成立,则称策略 $\pi'$ 优于策略 $\pi$;如果策略 $\pi^*$ 不差于其它任何一个策略,则称 $\pi^*$ 为最优策略($Optimal\ Policy$)
策略改进定理
设 $\pi$ 和 $\pi'$ 是一对确定性策略,且满足对任意 $s\in S$ 有$$
Q_\pi(s,\pi'(s))\ge V_{\pi'}(s) \tag{4-1}
$$
则策略 $\pi'$ 必定不差于策略 $\pi$;若存在至少一个状态使得严格不等式成立,则策略 $\pi'$ 必定优于策略 $\pi$证明:
对 ${\forall}s\in S$,根据动作值函数 $Q_\pi(s,a)$ 的定义
$$
\begin{aligned}
V_\pi(s)&\le Q_\pi(s,\pi'(s)) \\
~\\
&=E\left[R_{t+1}+\gamma\cdot V_\pi(s_{t+1})|S_t=s, A_t=\pi'(s)) \right]
\end{aligned}
$$
其中,动作 $a=\pi'(s)$,服从 $\pi'$ 分布,也就是求对策略 $\pi'$ 的期望,把 $\pi'$ 提到前面来$$
\begin{aligned}
&=E_{\pi'}\left[R_{t+1}+\gamma\cdot V_\pi(s_{t+1})|S_t=s) \right] \\
\end{aligned}
$$
再对其中的 $V_\pi(~)$ 重复前两步$$
\begin{split}
~\\
&\le E_{\pi'}\left[R_{t+1}+\gamma\cdot Q_\pi(s_{t+1},\pi'(s_{t+1}))|S_t=s \right] \\
~\\
&=E_{\pi'}\left[R_{t+1}+\gamma\cdot E_{\pi'}\left[R_{t+2}+\gamma\cdot V_\pi(s_{t+2}) |S_{t+1},A_{t+1}=\pi'(s_{t+1})\right]|S_t=s \right] \\
~\\
&=E_{\pi'}\left[R_{t+1}+\gamma\cdot R_{t+2}+\gamma^2\cdot V_\pi(s_{t+2})|S_t=s \right] \\
~\\
&\le E_{\pi'}\left[R_{t+1}+\gamma\cdot R_{t+2}+\gamma^2\cdot R_{t+3}+\gamma^3\cdot V_\pi(s_{t+3}) |S_t=s \right] \\
~\\
&\le \cdots \\
~\\
&\le E_{\pi'}\left[R_{t+1}+\gamma\cdot R_{t+2}+\gamma^2\cdot R_{t+3}+\cdots \gamma^{T-t-1}\cdot R_T|S_t=s \right] \\
~\\
&=V_{\pi'}(s) \\
~\\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Downarrow \\
~\\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ V_\pi(s)\le V_{\pi'}(s)
\end{split}
$$
策略改进算法
贪婪策略
$$
\pi'(s)=\mathop{\mathrm{\arg\max}}\limits_{a\in A}\ \ \mathcal{Q_\pi}(s,a) \tag{4-2}
$$
注意:贪婪策略必定满足公式(4-1)案例:
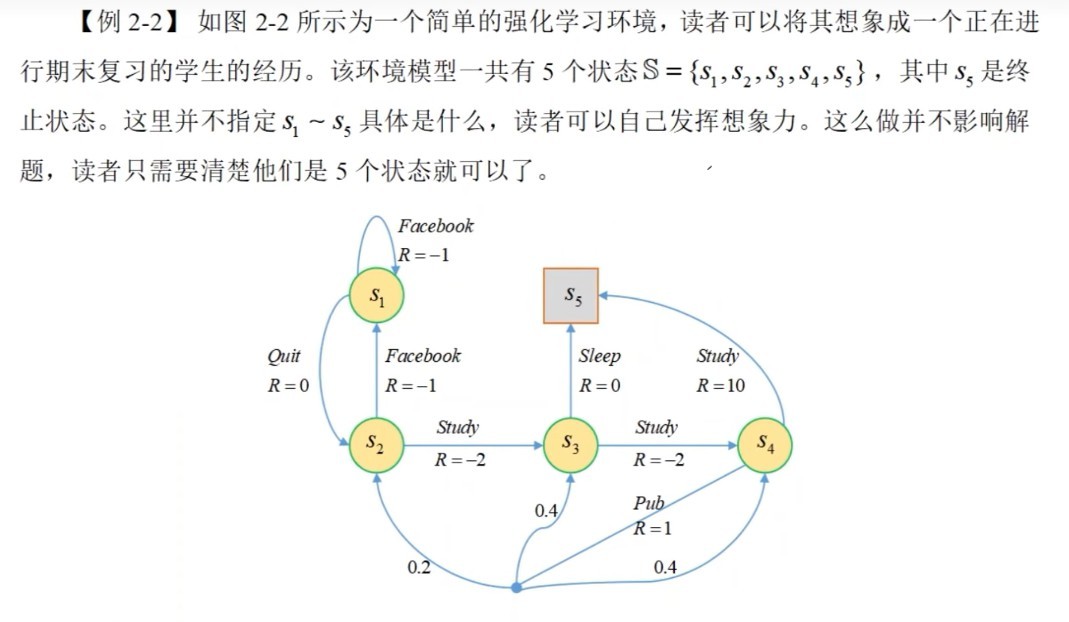
在第三节的案例中,已经得到了 $V_\pi(S_1)=-2.3077$,$V_\pi(S_2)=-1.3077$,$V_\pi(S_3)=2.6923$,$V_\pi(S_4)=7.3846$,由于该案例所有状态转移概率都是已知的,且 $\gamma=1$,根据公式(2-4)和公式(4-2)进行计算
$$
Q_\pi(s,a)=\sum_{s_{t+1}\in S}P(s_{t+1}|s,a)\cdot \left[R_{t+1}+\gamma\cdot V_\pi(s_{t+1})\right] \tag{2-4}
$$
(1). 当 $s=s_1$ 时,更优的策略是 $Quit$$$
Q(s_1,Quit)=1\times(0+V_\pi(s_2))=-1.3077 \\
~\\
Q(s_1,Facebook)=1\times(-1+V_\pi(s_1))=-3.3077 \\
~\\
\Downarrow \\
~\\
\begin{aligned}
\pi'(s_1)&=\mathop{\arg\max}\ \ \left({Q(s_1,Quit),Q(s_1,Facebook)}\right)\\
~\\
&=Quit\\
~\\
\end{aligned}
$$
(2). 当 $s=s_2$ 时,更优的策略是 $Study$$$
Q(s_2,Facebook)=-3.3077 \\
~\\
Q(s_2,Study)=0.6923 \\
~\\
\Downarrow \\
~\\
\begin{aligned}
\pi'(s_2)&=\mathop{\arg\max}\ \ (Q(s_2,Facebook),Q(s_2,study)) \\
~\\
&=Study
\end{aligned}
$$
(3). 当 $s=s_3$ 时,更优的策略是 $Study$$$
\cdots \\
\pi'(s_3)=Study
$$
(4). 当 $s=s_4$ 时,更优的策略是 $Study$$$
\cdots \\
\pi'(s_4)=Study
$$
综上所述,可以得到一个更优的策略$$
\pi'(s_1)=Quit \\
~\\
\pi'(s_2)=\pi'(s_3)=\pi'(s_4)=Study \\
$$
总结:利用动作值函数和状态值函数的关系(公式2-4),进行计算,利用动作值函数的大小进行评估参考
最后编辑于:2022 年 09 月 16 日 23:35
